병합 정렬이란 분할 정복 기법을 이용한 정렬기법 이다.
기본 개념은 일단 반으로나누고 나중에 합친다. 이것이 기본 개념이다.
시간 복잡도는 O(N*logN) 이다.
알고리즘
밑에 그림을 살펴보자 .
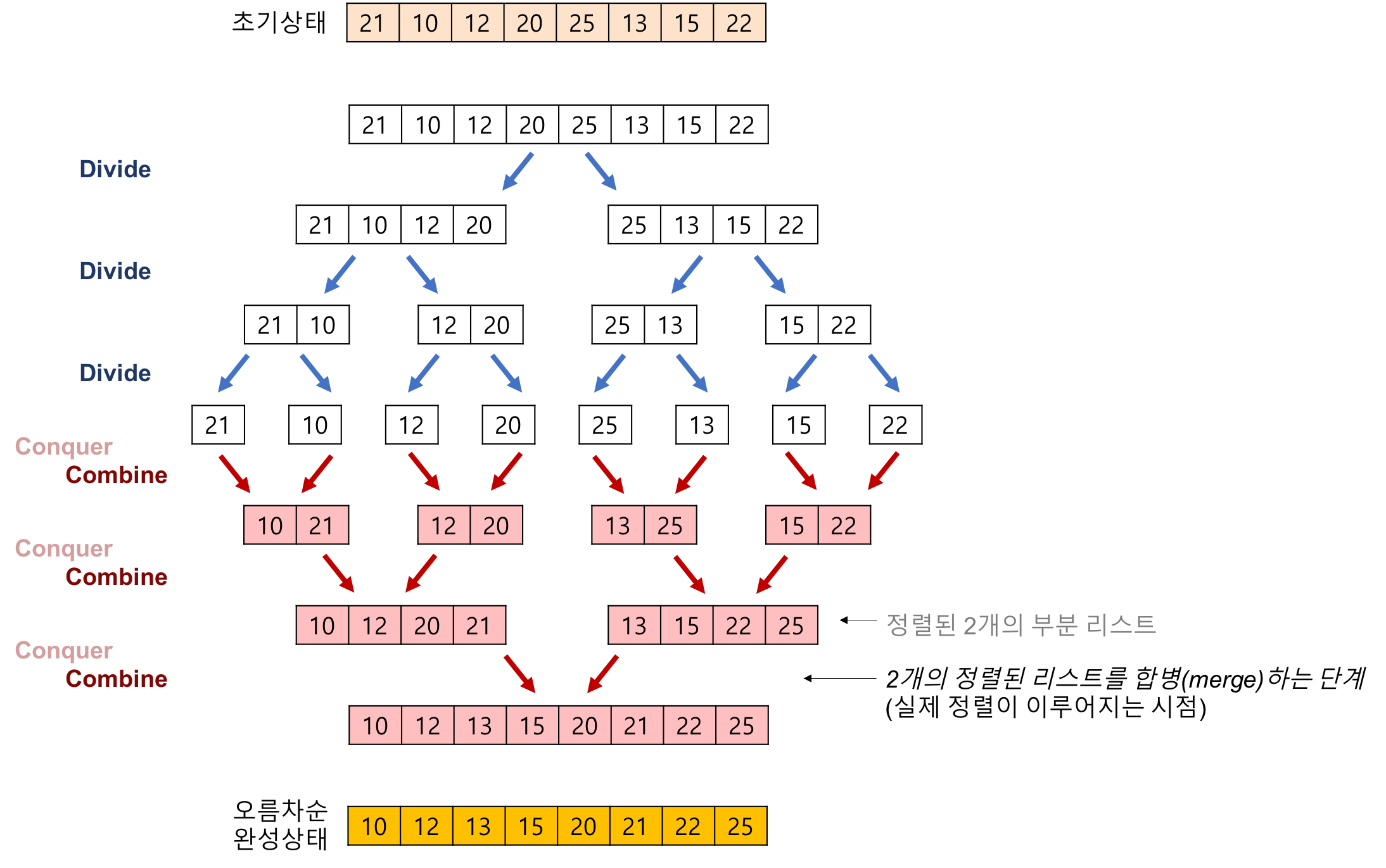
1. 초기 상태에서 더이상 반으로 나눌수 없을 때까지 계속 분할한다.
2. 그리고 다시 병합(merge) 할 때 크기를 비교하여 병합한다.
3. 병합을 모두 마무리하면 정렬이 완료된다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
# include <stdio.h>
# define MAX_SIZE 8
int sorted[MAX_SIZE]; // 추가적인 공간이 필요
// i: 정렬된 왼쪽 리스트에 대한 인덱스
// j: 정렬된 오른쪽 리스트에 대한 인덱스
// k: 정렬될 리스트에 대한 인덱스
/* 2개의 인접한 배열 list[left...mid]와 list[mid+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
void merge(int list[], int left, int mid, int right) {
int i, j, k, l;
i = left;
j = mid + 1;
k = left;
/* 분할 정렬된 list의 합병 */
while (i <= mid && j <= right) {
if (list[i] <= list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남아 있는 값들을 일괄 복사
if (i > mid) {
for (l = j; l <= right; l++)
sorted[k++] = list[l];
}
// 남아 있는 값들을 일괄 복사
else {
for (l = i; l <= mid; l++)
sorted[k++] = list[l];
}
// 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
for (l = left; l <= right; l++) {
list[l] = sorted[l];
}
}
// 합병 정렬
void merge_sort(int list[], int left, int right) {
int mid;
if (left < right) {
// 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
mid = (left + right) / 2;
// 앞쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, left, mid);
// 뒤쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, mid + 1, right);
// 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
merge(list, left, mid, right);
}
}
void main() {
int i;
const int n = MAX_SIZE;
int list[n] = { 21, 10, 12, 20, 25, 13, 15, 22 };
// 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
merge_sort(list, 0, n - 1);
// 정렬 결과 출력
for (i = 0; i < n; i++) {
printf("%d\n", list[i]);
}
}
|
cs |
모든 글의 내용은 나동빈님 블로그를 참고 하였습니다.
'c++ > 알고리즘 공부' 카테고리의 다른 글
| 계수 정렬 (Counting sort) (0) | 2020.05.08 |
|---|---|
| 힙 정렬 (Heap sort) (0) | 2020.05.08 |
| 퀵 정렬 : quick sort (0) | 2020.05.06 |
| 삽입 정렬 : insert sort (0) | 2020.05.06 |
| 버블 정렬 : Bubble sort (0) | 2020.05.06 |
병합 정렬이란 분할 정복 기법을 이용한 정렬기법 이다.
기본 개념은 일단 반으로나누고 나중에 합친다. 이것이 기본 개념이다.
시간 복잡도는 O(N*logN) 이다.
알고리즘
밑에 그림을 살펴보자 .

1. 초기 상태에서 더이상 반으로 나눌수 없을 때까지 계속 분할한다.
2. 그리고 다시 병합(merge) 할 때 크기를 비교하여 병합한다.
3. 병합을 모두 마무리하면 정렬이 완료된다.
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
# include <stdio.h>
# define MAX_SIZE 8
int sorted[MAX_SIZE]; // 추가적인 공간이 필요
// i: 정렬된 왼쪽 리스트에 대한 인덱스
// j: 정렬된 오른쪽 리스트에 대한 인덱스
// k: 정렬될 리스트에 대한 인덱스
/* 2개의 인접한 배열 list[left...mid]와 list[mid+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
void merge(int list[], int left, int mid, int right) {
int i, j, k, l;
i = left;
j = mid + 1;
k = left;
/* 분할 정렬된 list의 합병 */
while (i <= mid && j <= right) {
if (list[i] <= list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남아 있는 값들을 일괄 복사
if (i > mid) {
for (l = j; l <= right; l++)
sorted[k++] = list[l];
}
// 남아 있는 값들을 일괄 복사
else {
for (l = i; l <= mid; l++)
sorted[k++] = list[l];
}
// 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
for (l = left; l <= right; l++) {
list[l] = sorted[l];
}
}
// 합병 정렬
void merge_sort(int list[], int left, int right) {
int mid;
if (left < right) {
// 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
mid = (left + right) / 2;
// 앞쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, left, mid);
// 뒤쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, mid + 1, right);
// 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
merge(list, left, mid, right);
}
}
void main() {
int i;
const int n = MAX_SIZE;
int list[n] = { 21, 10, 12, 20, 25, 13, 15, 22 };
// 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
merge_sort(list, 0, n - 1);
// 정렬 결과 출력
for (i = 0; i < n; i++) {
printf("%d\n", list[i]);
}
}
|
cs |
모든 글의 내용은 나동빈님 블로그를 참고 하였습니다.
'c++ > 알고리즘 공부' 카테고리의 다른 글
| 계수 정렬 (Counting sort) (0) | 2020.05.08 |
|---|---|
| 힙 정렬 (Heap sort) (0) | 2020.05.08 |
| 퀵 정렬 : quick sort (0) | 2020.05.06 |
| 삽입 정렬 : insert sort (0) | 2020.05.06 |
| 버블 정렬 : Bubble sort (0) | 2020.05.06 |