파이썬 머신러닝 완벽 가이드 (권철민 저)을 요약정리했습니다.
회귀
통계학에서 회귀는 여러 개의 독립변수와 한 개의 종속 변수 간의 상관관계를 모델링하는 기법을 통칭한다.
회귀는 회귀계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러 가지 유형으로 나눌 수있다.
회귀에서 가장 중요한 것은 바로 회귀 계수인데, 이 회귀 계수가 선형이냐 아니냐에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다.
그리고 독립변수가 한 개인지 여러 개 인지에 따라 단일 회귀, 다중회귀로 나뉜다.
여러 가지 회귀 중에서는 선형 회귀가 가장 많이 사용 된다. 선형 회귀는 실제 값과 예측값의 차이(오류의 제곱값)를 최소화 하는 직선형 회귀선을 최적화하는 방식이다.
선형 회귀 모델은 규제방법에 따라 다시 별도의 유형으로 나뉠 수 있는데,
규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 패널티 값을 적용하는 것을 말합니다.
대표적인 선형 회귀 모델은 다음과 같습니다.
- 일반 선형 회귀 : 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화 할 수 있도록 회귀 계수를 최적화 하며, 규제(Regularization)를 적용하지 않은 모델입니다.
- 릿지(Rdige) 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델. L2 규제는 상대적으로 큰 회귀 계수 값의 영향도를 감소시키기 위해 회귀 계수 값을 더 작게 만든느 규제 모델입니다.
- 라쏘(Lasso): 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식. L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로만들어 회귀 에측 시 피처가 선택되지 않게 하는 것.
- 엘라스틱넷(ElasticNet) : L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터 셋에 적용되며, L1규제로 피처의 개수를 줄임과 동시에 L2규제로 계수 값의 크기를 조정
- 로지스틱 회귀 : 로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실 분류에 사용되는 선형모델.
일반적으로 이진 분류 뿐 아니라 희소 영역의 분류(ex. 텍스트 분류) 에서 뛰어난 예측 성능을 보임.
규제의 의미
규제의 효과를 보면 둘다 가중치의 성장을 제한하는 모습이다. 정확히는 감소하는 방향으로 진행하는 모습을 볼 수있다. 가중치의 성장을 제한한다는 것은 기존 학습에 큰 영향을 끼칠 수 있는 데이터를 지양하겠다는 의미로 볼 수 있다. 그렇다는건 데이터셋에서 볼 수 있는 일반적인 패턴이 아닌 몇몇 독특하면서 희소한 패턴을 가지는 데이터에 대한 영향을 덜 받겠다는 뜻이다. 대표적으로 이러한 데이터로 노이즈와 이상치가 있다.
L1과 L2 규제를 언제 사용해야 하나 ?
L1의 경우 가중치의 크기에 상관없이 상수값을 뺀다. 이는 대체적으로 불필요한 가중치의 수치를 0으로 만들도록 하는 방향으로 적용된다. 즉, 중요한 가중치만을 취하기 때문에 sparse featrue에 대한 모델을 구성하는데 적합하다.
L2의 경우 가중치의 값을 이용한다. 어느 정도 튀는 값에 대해 대응할 수 있다는 의미이다. 따라서 이상치나 노이즈가 있는 데이터에 대한 학습을 진행할 때 사용하면 좋다. 특히 선형 모델의 일반화에 좋다고 한다.
한줄요약! L1은 필요없는거는 쳐내고, L2는 일단 다가져간다 대신 다들 영향력을 좀 낮춰서.
단순 선형 회귀를 통한 회귀 이해
단순 선형 회귀는 독립변수도 하나, 종속변수도 하나인 선형 회귀이다.
예를 들어, 주택 가격이 주택의 크기로만 결정된다고 하자.
일반적으로 주택의 크기가 크면 가격이 높아지는 경향이 있기 때문에 다음과 같이 주택 가격은 주택 크기에 대해 선형의 관계로 표현할 수 있다.
X축이 주택의 크기 이고 Y축이 주택의 가격인 2차원 평면에서 기울기와 절편을 가진 1차 함수식으로 모델링 할 수 있다.
독립변수가 1개인 단순 선형 회귀에서는 이 기울기 W1과 절편W를 회귀 계수로 지칭한다.
그리고 회귀 모델을 이러한 1차 함수로 모델링 했다면 실제 주택 가격은 이러한 1차 함수 값에서 실제 값만큼의 오류값을 뺸 값 이된다 .
이렇게 실제 값과 회귀 모델의 차이에 따른 오류 값을 잔차라고 부른다.
최적의 회귀 모델을 만든다는 것은 바로 전체 데이터의 잔차 합이 최소고 되는 모델을 만드는 것이다.
일반적으로 오류 합을 계산 할 때는 절댓갑승ㄹ 취해 더하거나, 제곱을 구해서 더하는 방식을 취한다. 즉 Error ^2 = RSS 이다.
회구에서 RSS는 비용(Cost)이며 W 변수로 구성되는 RSS를 비용 함수라고 한다.
머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 오류값을 더 이상 감소하지 않는 최소의 오류 값을 구한느 것이다.
비용 최소화 - 경사하강법
경사 하강법의 사전적 의미인 ‘점진적인 하강’ 이라는 뜻에서도 알 수 있듯이, ‘점진적으로’ 반복적인 계산을 통해 W 파라미터 값을 업데이트 하면서
오류 값이 최소가 되는 W 파라미터를 구하는 방식입니다.
경사 하강법의 핵심은
“어떻게 하면 오류가 작아지는 방향으로 W값을 보정할 수 있을까?” 이다.
포물선 형태의 2차 함수의 최저점은 해당 2차 함수의 미분 값인 1차 함수의 기울기가 가장 최소일 때입니다.
예를 들어 비용 함수가 다음 그림과 같은 포물선 형태의 2차 함수라면 경사 하강법은 최초 W에서부터 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 W를 업데이트합니다.
마침내 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 W를 반환 합니다.
경사 하강법의 일반적인 프로세스는 다음과 같습니다.
- w0,w1을 임의의 값으로 설정하고 첫 비용 함수의 값을 계산합니다.
- w1을 실제값_i – 예측값_i , w0를 실제값_i – 예측값_i 로 업데이트 한 후 다시 비용함수의 값을 계산합니다.
- 비용 함수의 값이 감소했으면 다시 step2를 반복합니다. 더 이상 비용 함수의 값이 감소하지 않으면 그때의 w1,w0를 구하고 반복을 중지합니다.
경사하강법 구현 - 파이썬
간단한 회귀 식인 y= 4X + 6을 근사하기 위한 100개의 데이터 셋을 만들고,
여기에 경사 하강법을 이용해 회귀 계수 w1을 4에가까운 값으로, w0을 6에 가까을 값으로 도출 해보자.
import numpy as np
import matplotlib.pyplot as plt
X = 2*np.random.rand(100,1)
y = 6 +4*X+np.random.rand(100,1)
#X,y 데이터 셋 시각화
plt.scatter(X,y)데이터는 y= 4X + 6 을 중심으로 무작위로 퍼져있다.
이제 경사하강법을 이용해 y = w1 * x + w0에 해당하는 w1과 w0을 구해보자.
경사 하강법을 이용한 단순 선형 회귀는 w1 과 w0을 모두 0으로 초기화환 뒤 특정 횟수만큼 반복하면서 w1과 w0을 업데이트 한다.
먼저 w0와 w1을 업데이트할 값을 구하는 함수인 get_weight_update()를 생성하겠습니다.
# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환.
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update다음은 get_weight_updates()을 경사 하강 방식으로 반복적으로 수행하여 w1과 w0를 업데이트 하는 함수인
gradient_descent_steps() 함수를 생성하겠습니다.
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용함.
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0이제 gradient_descent_steps()를 호출해 w1과 w0를 구해 보겠습니다.
그리고 최종적으로 예측값과 실제값의 RSS차이를 계산하는 get_cost() 함수를 생성하고 이를 이용해 경사 하악법의 예측 오류도 계산해 보겠습니다.
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1: w0:".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:'.format(get_cost(y, y_pred)))w1:4.056 w0:6.420
Gradient Descent Total Cost:0.0786앞에서 구한 y_pred에 기반 해 회귀선을 그려 보겠습니다.
plt.scatter(X, y)
plt.plot(X,y_pred,'r')확률적 경사 하강법
확률적 경사 하강법은 전체 입력 데이터로 w가 업데이트되는 값을 계산하는 것이 아니라 일부 데이터만 이용해 w가 업데이트되는 값을 계산하므로 경사 하강법에 비해서 빠른 속도를 보장합니다.
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:'.format(get_cost(y, y_pred)))
w1: 4.055 w0: 6.415
Stochastic Gradient Descent Total Cost:0.0788확률적 경사 하강법으로 구한 w0, w1 결과는 경사 하강법으로 구한 w1,w0와 큰 차이가 없으며, 예측 오류 비용 또한 0.9937로
경사 하강법으로 구한 예측 오류 비용 0.9935 보다 아주 조금 높을 뿐으로 큰 예측 성능의 차이가 없을을 알 수 있다.
따라서 큰 데이터를 처리할 경우에는 경사 하강법은 매우 시간이 오래 걸리므로 일반적으로 확률적 경사 하강법을 이용한다.
ScikitLearn - LinearRegression을 이용한 보스턴 주택 가격 예측
사이킷런의 linear_models 모듈은 매우 다양한 졸유의 선형 기반 회귀를 클래스로 구현해 제공한다.
LinearRegression 클래스 - Ordinary Least Squares
LinearRegression 클래스는 예측값과 실제 값의 RSS를 최소화해 OLS 추정 방식으로 구현한 클래스이다. LinearRegression 클래스는 fit() 메서드로 X, y배열을 입력 받으면 회귀 계수인 W를 coef_ 속성에 저장한다 .
LinearRegression 클래스의 파라미터
입력 파라미터
- fit _intercept : boolen 값으로 디폴트는 true이다. 절편 값을 계산할 것인지 말지를 지정한다.
- normalize : boolen 값으로 디폴트는 False이다. 만일 True로 설정하면 회귀를 수행하기 전에 입력 데이터 셋을 정규화 한다.
속성
- coef_ = fit() 메서드를 수행했을 때 회귀 계수가 배열 형태로 저장하는 속서으.
- intercept_ : intercept 값
회귀 평가 지표
일반적으로 회귀의 성능을 평가하는 지표는 다음과 같다.
| 평가 지표 | 설명 |
|---|---|
| MAE | 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것 |
| MSE | 실제 값과 예측값의 차이를 제곱해 평균한 것 |
| RMSE | MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트를 씌운 것이 RMSE이다. |
| R^2 | 분산 기반으로 예측 성능을 평가. 실제 값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높다. |
사이킷런은 RMSE를 제공하지 않으므로, RMSE를 구하기 위해서는 MSE에 제곱근을 직접 씌워야 한다.
LinearRegression을 이용해 보스턴 주택 가격 회귀 구현
사이킷런에 내장된 데이터 셋인 보스턴 주택 가격 데이터를 이용한다.
피처에 대한 설명은 다음과 같다.
- CRIM : 지역별 범죄 발생률
- ZN : 25,000 평방피트를 초과하는 거주 지역 비열
- INDUS : 비상업 지역 넓이 비율
- CHAS : 찰스 강에 대한 더미 변수(강의 경계에 위치한 경우는1, 아니면 0)
- NOX : 일산화질소 농도
- RM : 거주할 수 있는 방 개수
- AGE: 1940년 이전에 건축된 소유 주택의 비율
- DIS : 5개 주요 고용 센터까지의 가중거리
- RAD : 고속도로 접근 용이도
- TAX : 10,000 달러다 재산세율
- PTRATIO : 지역의 교사와 학생 수 비율
- B : 지역의 흑인 거주 비율
- LSTAT : 하위 계층의 비율
- MEDV : 본인 소유의 주택 가격(중앙값)
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn.datasets import load_boston
%matplotlib inline
# boston 데이타셋 로드
boston = load_boston()
# boston 데이타셋 DataFrame 변환
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)
# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함.
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)
bostonDF.head()Boston 데이타셋 크기 : (506, 14)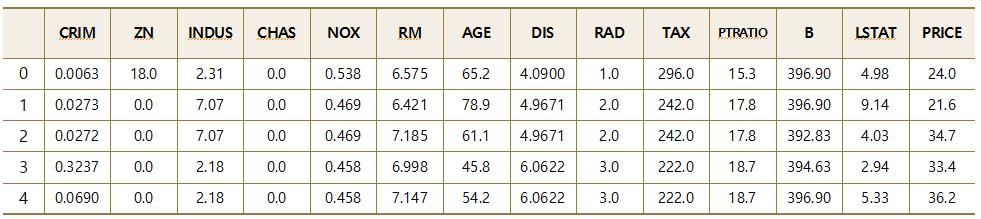
데이터 셋의 피처에 Null 값은 없으며 모두 float 값이다.
다음으로 각 칼럼이 회귀 결과에 미치는 영향이 어느 정도인지 시각화 해보자 .
‘RM’,‘ZN’,‘INDUS’,‘NOS’,‘AGE’,‘PTRATIO’,‘LSTAT’,‘RAD’의 총 8개의 칼럼에 대해 값이 증가할수록 PRICE 값이 어떻게 변하는지 확인하면 된다.
# 2개의 행과 4개의 열을 가진 subplots를 이용. axs는 4x2개의 ax를 가짐.
fig, axs = plt.subplots(figsize=(16,8) , ncols=4 , nrows=2)
lm_features = ['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i , feature in enumerate(lm_features):
row = int(i/4)
col = i%4
# 시본의 regplot을 이용해 산점도와 선형 회귀 직선을 함께 표현
sns.regplot(x=feature , y='PRICE',data=bostonDF , ax=axs[row][col])다른 칼럼보다 RM과 LSTAT의 PRICE 영향도가 두드러지게 나타난다.
이제 LinearRegression 클래스를 이용해 보스턴 주택 가격의 회귀 모델을 만들어 보자.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error , r2_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop('PRICE',axis=1,inplace = False)
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target,\
test_size = 0.3, random_state =156)
#선형 회귀 OLS로 학습/예측/평가 수행.
lr = LinearRegression()
lr.fit(X_train,y_train)
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test,y_preds)
rmse = np.sqrt(mse)
print('MSE : , RMSE : '.format(mse , rmse))
print('Variance score : '.format(r2_score(y_test, y_preds)))MSE : 17.297 , RMSE : 4.159
Variance score : 0.757LinearRegression 으로 생성한 주택 가격 모델의 intercept(절편)과 coefficients(회귀 계수) 값을 살펴 보겠습니다. 절편은 LinearRegression 객체의 intercept_속성에, 회귀 계수는 ceof_속성에 값이 저장돼 있습니다.
print('절편 값:',lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_, 1))절편 값: 40.99559517216467
회귀 계수값: [ -0.1 0.1 0. 3. -19.8 3.4 0. -1.7 0.4 -0. -0.9 0.
-0.6]coef_ 속성은 회귀 계수 값만 가지고 있으므로 이를 피처별 회귀 계수 값으로 다시 매핑하고, 높은 값순으로 출력해 보겠습니다. 이를 위해 판다스 Series의 sort_values() 함수를 사용합니다.
# 회귀 계수를 큰 값 순으로 정렬하기 위해 Series로 생성. index가 컬럼명에 유의
coeff = pd.Series(data=np.round(lr.coef_, 1), index=X_data.columns )
coeff.sort_values(ascending=False)RM 3.4
CHAS 3.0
RAD 0.4
ZN 0.1
B 0.0
TAX -0.0
AGE 0.0
INDUS 0.0
CRIM -0.1
LSTAT -0.6
PTRATIO -0.9
DIS -1.7
NOX -19.8
dtype: float64RM이 양의 값 으로 회귀 계수가 가장 크며, NOX 피처의 회귀 계수 - 값이 너무 크다.
최적화를 수행하면서 피처 상관계수의 변화도 함께 살펴 보자.
이번에는 5개의 폴드 셋에서 cross_val_score()를 이용해 교차 검증으로 MSE와 RMSE를 측정해 보자.
cross_val_score()의 인자로 scoring = ‘neg_mean_squared_error’를 지정하면 반환되는 수치 값은 음수 값입니다.
일반적으로 회귀는 MSE 값이 낮을수록 좋은 회귀 모델입니다.
사이킷런의 Scoring 함수를 호출하면 모델에서 계산된 MSE 값에 –1을 곱해야 양의 값인 원래 모델에서 계산된 MSE 값이 됩니다.
이렇게 다시 변형된 MSE 값에 넘파이의 sqrt() 함수를 적용해 RMSE를 구할 수 있습니다.
from sklearn.model_selection import cross_val_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
lr = LinearRegression()
# cross_val_score( )로 5 Fold 셋으로 MSE 를 구한 뒤 이를 기반으로 다시 RMSE 구함.
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# cross_val_score(scoring="neg_mean_squared_error")로 반환된 값은 모두 음수
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores, 2))
print(' 5 folds 의 평균 RMSE : '.format(avg_rmse))
5 folds 의 개별 Negative MSE scores: [-12.46 -26.05 -33.07 -80.76 -33.31]
5 folds 의 개별 RMSE scores : [3.53 5.1 5.75 8.99 5.77]
5 folds 의 평균 RMSE : 5.829 5개 폴드 셋에 대해서 교차 검증을 수행한 결과 ,평균 RMSE는 약 5.829가 나왔습니다.
cross_val_score(lr,X_data,y_target,scoring="neg_mean_squared_error")로 반환된 값을 확인해 보면 모두 음수임을 알 수 있습니다.





