플루이드 - 와샬 알고리즘은 그래프 탐색 알고리즘중 가장 간단하지만 모든 정점사이의 최단거리를 구할 수있다.
하지만 시간 복잡도가 O(N^3) 이므로 정점의 갯수가 많으면 쓰는데 제약이있다.
설명보다는 문제를 보면서 이해하는게 쉽다.
문제 링크 : https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 100)이 주어지고 둘째 줄에는 버스의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다. 시작
www.acmicpc.net
예제의 간선정보를 나타내보면
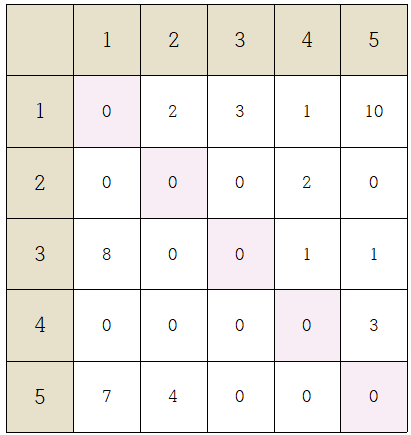
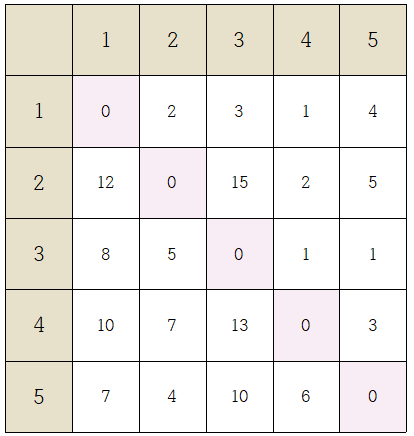
적용전 배열에 플루이드 와샬 알고리즘을 적용 해보자
알고리즘
|
1
2
3
4
5
6
7
8
|
//플로이드 와샬 알고리즘
for (int k = 0; k < N; k++) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = min(map[i][j], map[i][k] + map[k][j]);
}
}
}
|
for 문 세개로 알고리즘이 끝이다 그래서 가장간단하다고 생각했다.
문제에 대한 전체 소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
cin.tie(NULL);
ios::sync_with_stdio(false);
int N, M, map[101][101];
cin >> N >> M;
//배열 초기화
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == j)map[i][j] = 0;
else map[i][j] = 1000000000;
}
}
//간선 정보
for (int j = 0; j < M; j++) {
int a, b, c;
cin >> a >> b >> c;
map[a - 1][b - 1] = min(map[a - 1][b - 1], c);
}
//플로이드 와샬 알고리즘
for (int k = 0; k < N; k++) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
map[i][j] = min(map[i][j], map[i][k] + map[k][j]);
}
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (map[i][j] == 1000000000) map[i][j] = 0;
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cout << map[i][j] << " ";
}
cout << "\n";
}
cout << endl;
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
플루이드 알고리즘은 가장 간단하지만 시간이 오래걸려 사용할 수 있는 문제가 제한적 이다.
그에비해 다익스트라 알고림즘은 다소 복잡하지만 최단거리를 더 빠른시간내에 구할 수있기에 보통 문제에
다익스트라 알고리즘을 많이 적용 한다.
'c++ > 알고리즘 공부' 카테고리의 다른 글
| 삽입 정렬 : insert sort (0) | 2020.05.06 |
|---|---|
| 버블 정렬 : Bubble sort (0) | 2020.05.06 |
| 선택 정렬 : selection sort (0) | 2020.05.06 |
| DFS(깊이 우선 탐색) (0) | 2020.04.30 |
| BFS(너비 우선 탐색) (0) | 2020.04.30 |