백준 5719번: 거의 최단 경로

문제 링크 : https://www.acmicpc.net/problem/5719

5719번: 거의 최단 경로

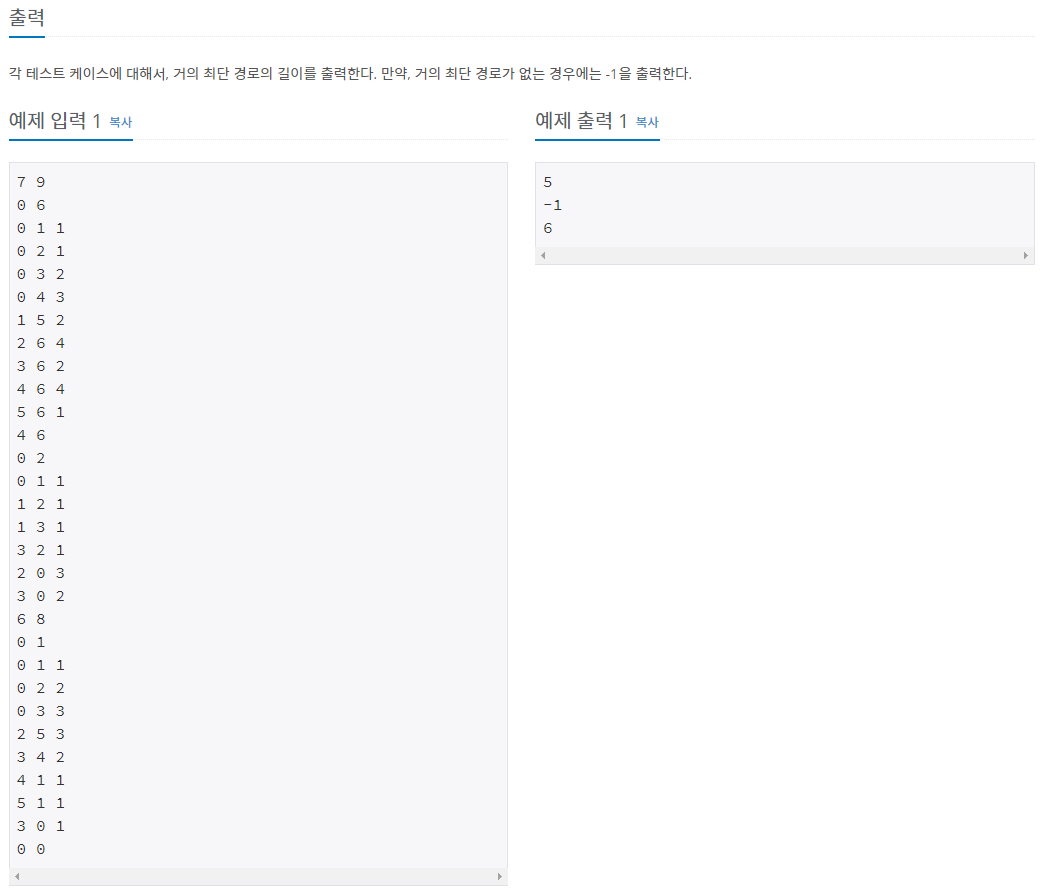
 문제 설명 

 

거의 최단경로 :  시작점에서 목적지 까지 가는 최단경로를 이용하지 않고 갈 수있는 최단 경로 .

 

1. 단방향 그래프가 주어지고 시작점과 목적지가 주어진다.

2. 현재 그래프에서 거의 최단경로를 구하여 거리 값을 출력하면됨 .

 

 

 알고리즘 

 

1. 다익스트라 알고리즘을 이용하여 최단 경로를 구한다.

2. 다익스트라 알고리즘에서 이용한 check배열을 이용하여 최단경로를 삭제한다.

3. 삭제한 그래프에서 다익스트라 알고리즘을 이용하여 최단경로를 구한다.

 

 코드  

 

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
int n, m, x, y, z, s, e;
int a[502][502];
int dp[502];
 
//다익스트라
//여기서는 이차원 배열로 구현하였는데 정점 최대의 갯수가 커지면 vector로구현해야함.
void dijkstra() {
 
    //배열 초기화
    memset(dp, -1, sizeof(dp));
    priority_queue<pair<int, int>> pq;
    pq.push({ 0,s });
    while (pq.size()) {
 
        int curr = pq.top().second;
        int dist = -pq.top().first;
        pq.pop();
        if (dp[curr] != -1)continue;
        dp[curr] = dist;
        for (int i = 0; i < n; i++) {
            if (a[curr][i] == -1)continue;
            if (dp[i] != -1)continue;
            pq.push({ -dist - a[curr][i],i });
        }
    }
}
 
 
//최단 경로 삭제 
void del() {
    queue<int> qu;
    qu.push(e);
 
    while (qu.size()) {
        int cx = qu.front();
        qu.pop();
 
        for (int i = 0; i < n; i++) {
            if (dp[cx] == dp[i] + a[i][cx] && a[i][cx] != -1) {
                a[i][cx] = -1;
                qu.push(i);
            }
        }
    }
}
int main() {
    scanf("%d%d", &n, &m);
    while (n != 0 && m != 0) {
        scanf("%d%d", &s, &e);
        memset(a, -1, sizeof(a));
        for (int i = 0; i < m; i++) {
            scanf("%d%d%d", &x, &y, &z);
            a[x][y] = z;
        }
 
        dijkstra();
        del();
        dijkstra();
 
        printf("%d\n", dp[e]);
        scanf("%d%d", &n, &m);
    }
 
    return 0;
}