Convolution
CNN을 다루기에 앞서 Convolution 연산의 의미와 쓰임에 대해 알아 보자.
왜 Convolution(CNN)을 쓰는가 ?
우선 우리가 왜 convolution(합성곱)을 써야하는지 부터 알아보면,
이전까지 배웠던 다층 신경망(MLP)는 fully connected 구조로, 가중치가 m x n의 행렬로 구성되어 있습니다.
즉, 입력벡터 x의 i번째 값을 업데이트 하기 이ㅜ해 $W_i$라는 긴 행이 필요했던 것이다.
요지는, 이게 당연하다고 생각했었는데 **사실은 메모리 측면에서 상당히 비효율 적이다.
층이 한두개가 아닐 텐데 이 fully-connected 구조가 수십개만 쌓여도 MLP구조는 메모리를 많이 차지하게 될 것이다. 그래서 이제부터 우리는 커널(kernel)을 기존의 행렬 대신 사용할 것이다. 커널은 필터(filter)로도 불린다. kernel은 크기가 훨씬 작은데도 x의 모든 요소에 대하여 적용할 수 있으므로 parameter size를 훨씬 줄일 수 있다.
모든 i에 대하여 적용 되는 커널은 V로 같고, 커널의 사이즈만큼 x상에서 이동하면서 적용한다.
이것도 선형식으로 나타내어지는 연산이기 때문에 convolution 연산도 당연히 선형변환에 속한다.
Convolution 연산
Convolution 연산의 수학적인 의미는 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링 하는것 이다.
여기서 국소적이라는 말은 특정 영역으로 해석하면, 결국 kernel 사이즈만큼의 데이터를 증폭 또는 감소시킨다고 해석할 수 있 을 것같다. 식으로는 아래와 같이 나타낼 수 있다.
다차원에서의 convolution
당장 이미지만 해도, 2차원 처럼 보이지만 RGB값이나 투명도 채널까지 고려하려면 3차원 이상의 데이터로 변하게 된다.
다양한 데이터를 처리하려면 다차원에서의 convolution 방법도 알아야 한다.
- 1D-conv
$f*g=\sum\limits_{p=1}^d f(p)g(i+p)$ - 2D-conv
$f*g(i,j)=\sum\limits_{p,q} f(p,q)g(i+p, j+q)$ - 3D-conv
$f*g(i,j,k)=\sum\limits_{p,q,r} f(p,q,r)g(i+p,j+q,k+r)$
여전히 $i,j,k$ 값이 바뀌어도 커널 $f$의 값은 바뀌지 않는다는 점에 주목하자.
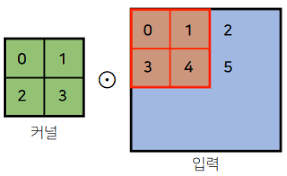
위와 같은 커널에서 만들어지는 출력은 2 x 2 크기이고 (1,1) entry 값은 19,(1,2) entry 값은 25임을 쉽게 알 수 있다.
그래서 2D conv에서 입력의 크기를 (H,W), 커널 크기를$(K_H,K_W)$, 출력의 크기를 $(O_H,O_W)$라고 하면 아래와 같은 식을 쉽게 유도해 낼 수 있다.
$O_H = H - K_H + 1$
$O_W = H - K_W + 1$
예를 들어 28 x 28 입력을 3 x 3 kernel로 2D-Conv 연산을 하면 26 x 26이 된다.
3차원 convolution의 경우 2차원 convolution을 3번 적용한다고 생각하면 된다.
참고로 3차원부터는 입력이나 커널이 2차원 행렬로 나타내어지지않기 때문에 이들을 텐서라고 부른다.
여기서는 모든 채널에 대하여 2차원에서의 convolution을 똑같이 적용하고 그것을 다 더해주면 된다.
물론 커널의 채널 수와 입력의 채널 수가 같아야 한다.
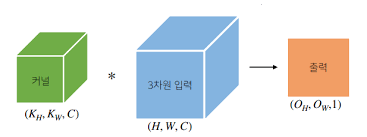
위와 같이 출력이 1차원으로 나오게되는데, 만약 출력 채널을 $O_C$개로 늘리고 싶으면 커널을 $O_C$개 사용하면 된다.
역전파
Convolution 연산도 커널(필터)의 parameter 갱신이 필요한다.
위 블로그에 설명이 잘 되어있기 때문에 생략 ..
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| 신경망과 역전파 (0) | 2021.03.11 |
|---|---|
| Optimizer(최적화) (0) | 2021.03.10 |
Convolution
CNN을 다루기에 앞서 Convolution 연산의 의미와 쓰임에 대해 알아 보자.
왜 Convolution(CNN)을 쓰는가 ?
우선 우리가 왜 convolution(합성곱)을 써야하는지 부터 알아보면,
이전까지 배웠던 다층 신경망(MLP)는 fully connected 구조로, 가중치가 m x n의 행렬로 구성되어 있습니다.
즉, 입력벡터 x의 i번째 값을 업데이트 하기 이ㅜ해 $W_i$라는 긴 행이 필요했던 것이다.
요지는, 이게 당연하다고 생각했었는데 **사실은 메모리 측면에서 상당히 비효율 적이다.
층이 한두개가 아닐 텐데 이 fully-connected 구조가 수십개만 쌓여도 MLP구조는 메모리를 많이 차지하게 될 것이다. 그래서 이제부터 우리는 커널(kernel)을 기존의 행렬 대신 사용할 것이다. 커널은 필터(filter)로도 불린다. kernel은 크기가 훨씬 작은데도 x의 모든 요소에 대하여 적용할 수 있으므로 parameter size를 훨씬 줄일 수 있다.
모든 i에 대하여 적용 되는 커널은 V로 같고, 커널의 사이즈만큼 x상에서 이동하면서 적용한다.
이것도 선형식으로 나타내어지는 연산이기 때문에 convolution 연산도 당연히 선형변환에 속한다.
Convolution 연산
Convolution 연산의 수학적인 의미는 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링 하는것 이다.
여기서 국소적이라는 말은 특정 영역으로 해석하면, 결국 kernel 사이즈만큼의 데이터를 증폭 또는 감소시킨다고 해석할 수 있 을 것같다. 식으로는 아래와 같이 나타낼 수 있다.
다차원에서의 convolution
당장 이미지만 해도, 2차원 처럼 보이지만 RGB값이나 투명도 채널까지 고려하려면 3차원 이상의 데이터로 변하게 된다.
다양한 데이터를 처리하려면 다차원에서의 convolution 방법도 알아야 한다.
- 1D-conv
$f*g=\sum\limits_{p=1}^d f(p)g(i+p)$ - 2D-conv
$f*g(i,j)=\sum\limits_{p,q} f(p,q)g(i+p, j+q)$ - 3D-conv
$f*g(i,j,k)=\sum\limits_{p,q,r} f(p,q,r)g(i+p,j+q,k+r)$
여전히 $i,j,k$ 값이 바뀌어도 커널 $f$의 값은 바뀌지 않는다는 점에 주목하자.

위와 같은 커널에서 만들어지는 출력은 2 x 2 크기이고 (1,1) entry 값은 19,(1,2) entry 값은 25임을 쉽게 알 수 있다.
그래서 2D conv에서 입력의 크기를 (H,W), 커널 크기를$(K_H,K_W)$, 출력의 크기를 $(O_H,O_W)$라고 하면 아래와 같은 식을 쉽게 유도해 낼 수 있다.
$O_H = H - K_H + 1$
$O_W = H - K_W + 1$
예를 들어 28 x 28 입력을 3 x 3 kernel로 2D-Conv 연산을 하면 26 x 26이 된다.
3차원 convolution의 경우 2차원 convolution을 3번 적용한다고 생각하면 된다.
참고로 3차원부터는 입력이나 커널이 2차원 행렬로 나타내어지지않기 때문에 이들을 텐서라고 부른다.
여기서는 모든 채널에 대하여 2차원에서의 convolution을 똑같이 적용하고 그것을 다 더해주면 된다.
물론 커널의 채널 수와 입력의 채널 수가 같아야 한다.

위와 같이 출력이 1차원으로 나오게되는데, 만약 출력 채널을 $O_C$개로 늘리고 싶으면 커널을 $O_C$개 사용하면 된다.
역전파
Convolution 연산도 커널(필터)의 parameter 갱신이 필요한다.
위 블로그에 설명이 잘 되어있기 때문에 생략 ..
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| 신경망과 역전파 (0) | 2021.03.11 |
|---|---|
| Optimizer(최적화) (0) | 2021.03.10 |

