신경망과 역전파

우선 신경망에 대해 다루기 전, 선형모델과 비선형 모델의 차이점부터 짚고 넘어가자.

선형 모델과 비선형 모델

참고블로그

일반적으로 y와 x의 관계가 일차식이면 모두 선형모델이라고 착각하기 쉽다.

우리가 관심을 가져야할 것은 x로 나타낸식이 일차식이냐 아니냐가 아니라 우리가 추정할 대상인 파라미터가 어떻게 생겼느냐이다.
예를 들어, 어떤 파라미터 뒤의 다항식이 $x^2$이더라도 $x^2$을 $x_r$로 치환해버리면 그만이다.
선형 모델은 문자항이 아닌 파라미터 부분이 선형식으로 표현되는 모델이다.

좀더 자세히 알아보면,
선형 회귀 모델은 '회귀 계수(regression coefficient)를 선형 결합으로 표현할 수 있는 모델'을 말한다. 즉 독립 변수가 일차식이냐 이차식이냐 로그 함수식이냐가 아니라 우리가 추정할 대상인 파라미터가 어떻게 생겼느냐의 문제이다. 가령 아래 함수들은 모두 선형 회귀 식이다.

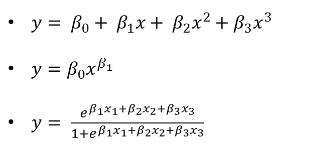
예를 들어 첫번째 식의 경우 독립변수인 x를 기준으로 생각하면 $x^2,x^3$ 때문에 비선형이라고 생각하기 쉽지만, 앞서 언급했듯이 회귀 모델의 선형성은 x 가 아니라 회귀 게수인 베타0,베타1,베타2,베타3을 기준으로 생각하는 것이기 때문에 이 기준으로 보면 선형 회귀식이다.
게다가 위 식들은 모두 '선형성'에 직접적으로 관련되지 않은 변수인 x와 y를 적절히 변환할 경우 모두 선형 회귀식으로 표현이 가능하다.

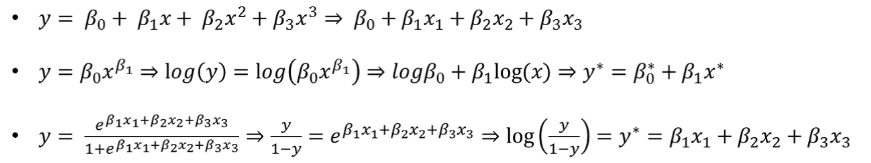
비록 위와 같은 데이터 변환을 통해 선형 회귀식으로 표현가능한 회귀식을 좀 더 엄밀하게는 linearizable regression model이라고 부르기도 하지만 포괄적으로 봤을 때는 그냥 선형 회귀 모델이라고 부르는 것이 맞다. 왜냐하면 linearizable regression model의 파라미터를 추정할 때도 일반적인 선형 회귀 모델과 동일한 기법을 사용하기 때문이다.

그렇다면 비선형 회귀 모델은 무엇일까 ?
비선형 모델은 데이터를 어떻게 변형하더라도 파라미터를 선형 결합식으로 표현할 수 없는 모델을 말한다. 이런 비션형 모델 중 단순한 에로는 아래와 같은 것이 있다. 이 식은 아무리 x,y변수를 변환하더라도 파라미터를 선형식으로 표현할 수 없다.

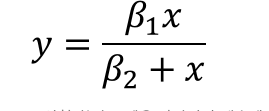
선형 회귀 모델은 파라미터 계수에 대한 해석이 단순하지만 비선형 모델은 모델의 형태가 복잡할 경우 해석이 매우 어렵다. 그래서 보통 모델의 해석을 중시하는 통계 모델링에서는 비선형 회귀 모델을 잘 사용하지 않는다.
그런데 만약 회귀 모델의 목적이 해석이 아니라 예측에 있다면 비선형 모델은 상당히 유연하기 때문에 복잡한 패턴을 갖는 데이터에 대해서도 모델링이 가능하다. 그래서 충분히 많은 데이터를 갖고 있어서 varaincae error를 충분히 줄일 수 있고 예측 자체가 목적인 경우라면 비선형 모델은 사용할만한 도구이다.

정리하자면, 선형 회귀 모델은 파라미터가 선형식으로 표현되는 회귀 모델을 의미한다. 그리고 이러한 선형 회귀 모델은 파라미터를 추정하거나 모델을 해석하기가 비선형 모델에 비해 비교적 쉽게 때문에, 데이터를 적절히 변환하거나 도움이 되는 feature를 추가하여 선형 모델을 만들 수 있다면 이렇게 하는 것이 적은 개수의 feature로 복잡한 비선형 모델을 만드는 것 보다 여러 면에서 유리하다.

어떤 식을 선형모델로 표현할 수 없는 경우 파라미터의 결합 형태가 복잡하여 선형 모델로 표현할 수 없을 때 발생한다.
딥러닝에서는 파라미터의 결합 형태가 매우 다양하기 때문에, 선형 모델만으로 표현할 수 없는 모델은 비선형모델을 사용한다.

신경망의 수식 표현

보통 신경망이라고 하면 아래와 같은 형태를 떠올릴 것이다.

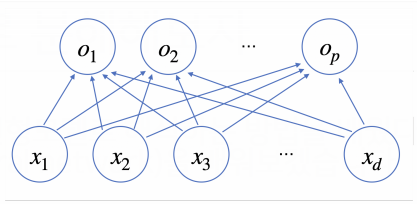
각 $x_i(1<=i<=d)$에서 $p$개의 $o_j(1<=j<=p)$노드로 화살표를 쏘아주는데, 각 화살표에는 고유의 가중치 값 $w_{ij}$가 존재한다.
즉, $x_i$ 노드에 $w_{ji}$가 곱해진 값이 $o_j$에 더해지는 것이다. 따라서 아래 식이 성립한다.

$o_{j}$ = $\sum\limits^{d}_{i=1}$ $x_{i}w_{ji}$

n개의 입력에 대한 출력 값을 동시에 얻기 위해 이를 행렬로 써주면 아래와 같다. 출력 벡터의 차원이 d에서 p로 바뀌게 된다.

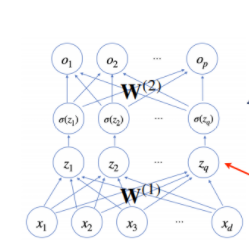
위 신경망 이미지를 기준으로 각 $x_i$는 $x_1,x_2,...,x_d$로 이루어져 있으며, 각 $o_j$는 $o_1,o_2,...,o_p$로 이루어져있다는 점에 유의한다. 우리는 하나의 입출력 데이터가 아닌 여러 입출력 데이터를 다룰 것이며 그렇기 때문에 행렬을 통해 연산을 표현하는 것이다.
b는 절편값을 나타내는 행렬로, 모든 행이 같은 값을 가진다.

softmax 함수

소프트맥스 함수는 각 input을 0과 1사이의 값으로 정규화 해주며 정규화돤 값의 합은 1이 된다.
즉, 이 함수는 모델의 출력을 확률로 해석할 수 있게 변환해준다.
$p_{i}=\frac{\text{exp}(o_{i})}{\sum_{k=1}^{p} \text{exp}(o_{k})} \ \text{for}\ i=1, 2, ... k$
$\text{softmax}(\text{o})=\left(\frac{\text{exp}(o_{1})}{\sum_{k=1}^{p} \text{exp}(o_{k})}, \cdots ,\frac{\text{exp}(o_{p})}{\sum_{k=1}^{p} \text{exp}(o_{k})}\right) = \left(p_{1}, \cdots, p_{k}\right) = \hat{y}$

softamx 함수의 paramter로는 당연히 이전에 구한 o벡터, 즉 $Wx + b$가 들어갈 것이다.

분류 문제를 풀 때 선형모델과 소프트맥스 함수를 경합하여 예측한다. 학습시킬 때는 softmax 함수를 사용하나, 실제 추론할 때는 one-hot벡터로 최댓값을 가진 주소만 1로 출력하는 연산을 사용한다.

활성함수

활섬 함수(activation function)는 실수 위에 정의된 비선형함수로, 신경망에서 입력받은 데이터를 다음층으로 출력할지를 결정한다.
활섬함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없다. 뉴런은 임계치를 넘을때만 값을 출력해야하며, 그과정에서 활성함수를 사용한다.
과거에는 sigmoid 함수와 tanh를 많이 사용하였으나, 최근에는 보통 ReLU함수를 많이 사용한다.

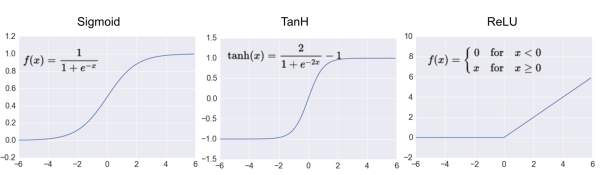
sigmoid함수와 tanh함수는 기울기 소실 문제로 인해 잘 사용하지 않는다.

활성 함수는 어떤 한 층을 지나고 나온 출력값에 적용한다.
이후 해당 출력은 다음 층의 입력으로 들어가게 된다.
따라서 신경망은 선형모델과 활성 함수를 합성한 함수라고 볼 수 있다.

층을 여러개 쌓는 이유 ?

• 이론적으로 2층 신경망으로도 임의의 연속함수를 근사할 수 있다.
• 그러나 실제 적용에서는 2층만으로는 무리가 있다. 층이 깊을수록 목적함수로 근사하는데 있어 필요한 노드의 갯수가 빠르게 줄어들기 때문에 층이 깊어질수록 적은 parameter로 복잡한 함수를 표현할 수 있다. 즉, 층이 얇으면 신경망의 너비가 늘어나게 된다.
• 하지만 층이 깊다고 정확도가 꼭 좋은것은 아니다. 최적화가 어려워지며 특히 활성 함수를 여러번 통과하면 유의미한 값이 사라질 가능성도 있다.

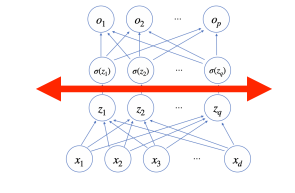
지금까지 살펴본 것은 신경망의 순전파(forward propagation)이다.

역전파 알고리즘

---

Backpropagation은 신경망을 학습시키기 위한 일반적인 알고리즘 중 하나이다.
내가 뽑고자하는 target 값과 실제 모델이 계산한 output이 얼마나 차이가 나는지 구한 후 그 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신하는 알고리즘인 것이다.

딥러닝은 역전파(backpropagation) 알고리즘을 이용하여 각 층에 사용된 파라미터 W와 b를 학습합니다. 역전파는 손실 함수를 W에 대한 그레디언트 값을 계산할 때 사용됩니다. 이때, 합성함수의 미분법인 연쇄 법칙(chain-rule)을 기반으로 자동 미분(auto-differentiation)을 사용합니다. 각 노드의 텐서 값을 컴퓨터가 기억하고 있어야 미분 계산이 가능합니다. 그래서 역전파 알고리즘은 메모리 사용량이 많이 필요로 합니다.

역전파 알고리즘 이해하기 !